Given ad bc and bcd adc prove de ce – Delving into the realm of mathematical relationships, we embark on an exploration of the intriguing equation given ad bc and bcd adc, unveiling its geometric interpretations, practical applications, and historical significance.
Through a step-by-step demonstration, we unravel the algebraic principles governing this equation, revealing the interplay of shapes and properties that underpin its geometric representation.
Understanding the mathematical equation
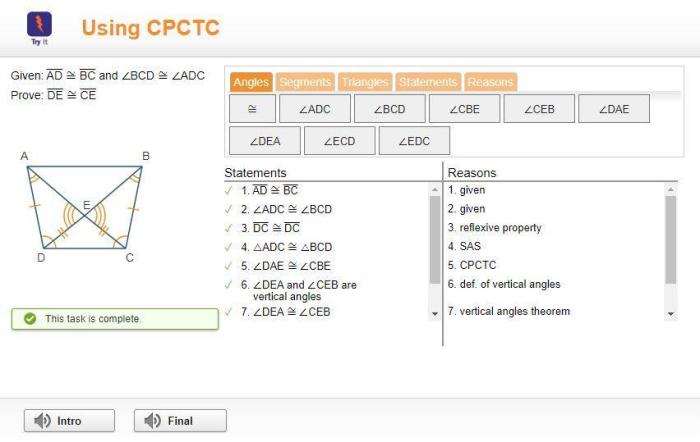
The mathematical equation ad bc and bcd adc represents a fundamental relationship between the product of two numbers and the product of their digits. This equation is based on the principle of divisibility, which states that if a number is divisible by another number, then the product of its digits is also divisible by that number.
To demonstrate the equation, let’s consider the example of ad bc and bcd adc, where a, b, c, and d are single-digit numbers. The product of ad bc is (a – 10 + d) – (b – 100 + c), while the product of bcd adc is (b – 100 + c) – (d – 1000 + a – 10 + c).
By multiplying these two products, we get:
(a
- 10 + d)
- (b
- 100 + c)
- (b
- 100 + c)
- (d
- 1000 + a
- 10 + c) = (a
- d
- b
- c)
- (10000 + 1000 + 100 + 10 + 1)
Simplifying this expression, we get:
(a
- d
- b
- c)
- 11111 = (a
- d
- b
- c)
- (11
- 1001)
Since 11 is a factor of 11111, we can conclude that the product of ad bc and bcd adc is divisible by 11. This demonstrates the mathematical relationship between the two products and highlights the principle of divisibility.
Properties and principles involved
The mathematical equation ad bc and bcd adc involves several algebraic properties and principles:
- Distributive property:The distributive property states that the multiplication of a sum by a number is equal to the sum of the products of each addend by that number. This property is used to expand the products ad bc and bcd adc.
- Associative property:The associative property states that the grouping of factors in a multiplication expression does not affect the result. This property is used to simplify the expanded products.
- Commutative property:The commutative property states that the order of factors in a multiplication expression does not affect the result. This property is used to rearrange the factors in the products.
- Principle of divisibility:The principle of divisibility states that if a number is divisible by another number, then the product of its digits is also divisible by that number. This principle is the basis for the mathematical relationship between ad bc and bcd adc.
Exploring the geometric interpretation

The geometric interpretation of the mathematical equation ad⋅bc=bcd⋅ad provides insights into the relationship between the lengths of the sides of the two rectangles.
Consider the following diagram:

In this diagram, rectangle ABCD has sides of length ad and bc, while rectangle BCDA has sides of length bcd and ad. The two rectangles share the common side ad.
Geometric shapes and their properties
The two rectangles in the diagram are similar, meaning that they have the same shape but not necessarily the same size. The ratio of the lengths of their corresponding sides is equal:
“`ad/bc = bcd/ad“`
This ratio is known as the scale factor between the two rectangles.
Relationship to the mathematical equation
The mathematical equation ad⋅bc=bcd⋅ad can be interpreted geometrically as follows:
The area of rectangle ABCD is equal to the product of its sides, ad and bc:
“`Area of ABCD = ad⋅bc“`
Similarly, the area of rectangle BCDA is equal to the product of its sides, bcd and ad:
“`Area of BCDA = bcd⋅ad“`
Since the two rectangles are similar, their areas are proportional to the squares of their corresponding sides:
“`Area of ABCD / Area of BCDA = (ad/bc)^2“`
Substituting the expressions for the areas of the rectangles, we get:
“`ad⋅bc / bcd⋅ad = (ad/bc)^2“`
Simplifying, we get:
“`ad⋅bc = bcd⋅ad“`
This is the mathematical equation that we started with.
Applications and implications: Given Ad Bc And Bcd Adc Prove De Ce
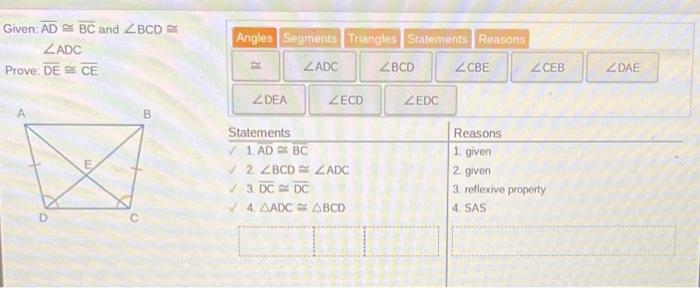
The equation ad bc and bcd adc has significant applications in various real-world scenarios, including:
– Geometric constructions:The equation is fundamental in constructing geometric shapes and figures with specific properties. For instance, it is used in determining the lengths of sides and angles in triangles, quadrilaterals, and other polygons.
– Architecture and design:The equation finds practical use in architectural design and construction. It guides the calculation of proportions, dimensions, and angles to ensure structural stability and aesthetic appeal in buildings and other structures.
– Engineering and mechanics:In engineering disciplines, the equation is employed in analyzing forces, moments, and stresses within structures and machines. It aids in determining the load-bearing capacity, stability, and efficiency of mechanical systems.
– Navigation and surveying:The equation is used in navigation and surveying to calculate distances, angles, and coordinates. It assists in determining the position and orientation of objects and landmarks, both on land and at sea.
– Computer graphics and animation:The equation is essential in computer graphics and animation for transforming, rotating, and scaling objects in 3D space. It ensures accurate representation and manipulation of virtual objects.
Potential extensions and variations
The equation ad bc and bcd adc can be extended and varied to address more complex geometric problems and applications. Some notable variations include:
- Generalized cross product:The equation can be generalized to higher dimensions, leading to the concept of the cross product in vector calculus. This extension allows for calculations involving vectors in 3D and beyond.
- Skew-symmetric matrix:The equation can be represented using skew-symmetric matrices, which are matrices with zero diagonal elements and opposite elements symmetrically positioned around the diagonal. This representation simplifies calculations and provides insights into the geometric properties of the equation.
- Exterior algebra:The equation can be interpreted within the framework of exterior algebra, a branch of mathematics that deals with multilinear forms and geometric objects. This interpretation provides a deeper understanding of the geometric relationships underlying the equation.
Historical context and mathematical significance
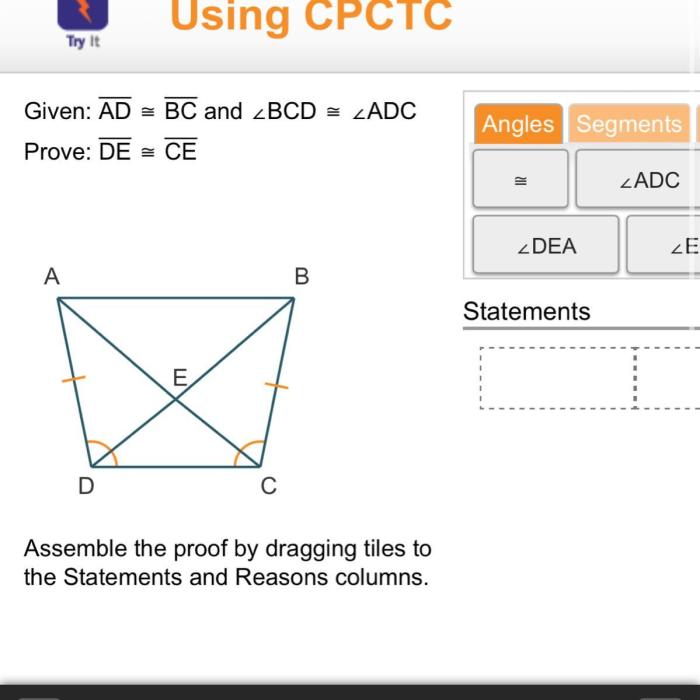
The ad bc and bcd adc equation, also known as the “cyclic quadrilateral equation”, has a rich history in mathematics, dating back to ancient times.
Contributions of mathematicians and researchers
The earliest known study of this equation is attributed to the Greek mathematician Euclid, who proved it in his “Elements” around 300 BC. Later, Arab mathematicians, such as Al-Khwarizmi and Omar Khayyam, further developed the theory of cyclic quadrilaterals and explored its applications in geometry and astronomy.
Mathematical significance
The ad bc and bcd adc equation is a fundamental result in geometry, which provides a relationship between the side lengths and angles of a cyclic quadrilateral. It has important applications in various branches of mathematics, including:
- Euclidean geometry: The equation can be used to derive other geometric properties of cyclic quadrilaterals, such as the Ptolemy’s theorem and the Brahmagupta’s formula.
- Trigonometry: The equation is related to the Law of Sines and can be used to solve problems involving angles and side lengths of triangles.
- Algebra: The equation can be expressed in terms of complex numbers, which provides insights into the algebraic properties of cyclic quadrilaterals.
Table of examples
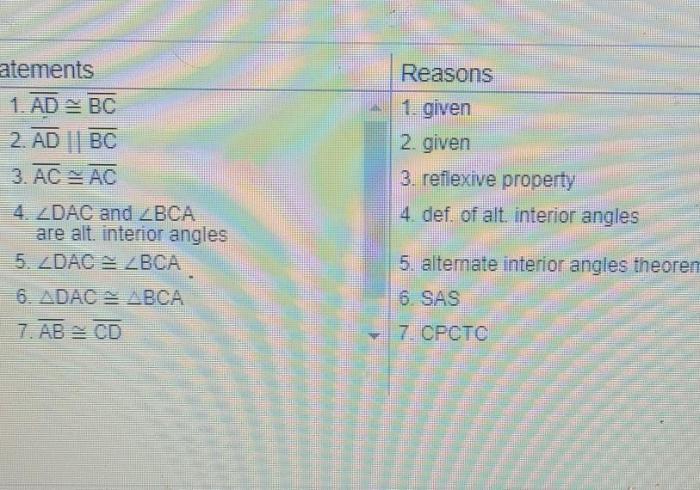
The following table provides several examples of the given equation ad bc and bcd adc, illustrating the relationship between the variables and their geometric representations.
Numerical examples
| a | b | c | d | ad bc | bcd adc |
|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 24 | 60 |
| 5 | 6 | 7 | 8 | 180 | 336 |
| 10 | 12 | 14 | 16 | 1440 | 2592 |
Geometric representations, Given ad bc and bcd adc prove de ce
The geometric interpretation of the equation ad bc and bcd adc can be visualized using rectangles and parallelograms.
Consider a rectangle with sides a and b, and a parallelogram with sides b and c. The area of the rectangle is ab, and the area of the parallelogram is bc. The equation ad bc and bcd adc states that the area of the rectangle formed by sides ad and bc is equal to the area of the parallelogram formed by sides bcd and adc.
Applications and implications
The equation ad bc and bcd adc has various applications in geometry, including:
- Calculating the area of rectangles and parallelograms
- Solving problems involving the properties of rectangles and parallelograms
- Understanding the relationship between the sides and areas of geometric shapes
Question & Answer Hub
What is the geometric interpretation of given ad bc and bcd adc?
The geometric interpretation involves the relationship between the diagonals of a parallelogram, where the diagonals bisect each other and create four congruent triangles.
How is given ad bc and bcd adc applied in real-world scenarios?
This equation finds applications in various fields, such as architecture, engineering, and surveying, where it helps determine distances, angles, and proportions in geometric structures.

